Trigonometric Identities
A-Level
What are trigonometric identities?
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variable where both sides are defined. They’re not just abstract facts to memorize—they’re powerful tools for simplifying expressions, solving equations, and proving relationships in both pure and applied maths.
Why do I need to learn trigonometric identities?
At A-Level, identities appear in:
-
Simplifying complex expressions
-
Solving trigonometric equations
-
Calculus (differentiation/integration of trig functions)
-
Mechanics and wave modelling
Understanding them deeply—not just memorizing—will save you time and boost your confidence in exams.
Core Identities:
1. Reciprocal Identities
2. Quotient Identity
3. Pythagorean Identities
4. Compound & Double Angle Identities
1. Reciprocal Identities


Proof:
csc, sec and cot are simply the reciprocal of sin, cos and tan.
The reciprocal means you divide 1 by it, as demonstrated here:
Example:
Simplify the expression:

Recall the reciprocal identities

Substitute: replace each reciprocal function with its trigonometric equivalent:

Final answer:
This is the simplified form. You’ve used reciprocal identities to convert the expression into basic trigonometric functions—much easier to work with in equations or calculus.
2. Quotient Identity

Example:
Simplify the following expression

Recall the quotient identify and reciprocal identity

Substitute back into the expression:

Giving the final answer:

3. Pythagorean Identities

Prove:
Recall:

Square both recalled terms:

Add them together:
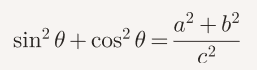
Recall Pythagorean theorum:
Substituting gives us:

Which proves:
Prove:
Recall:

Square both:

Add 1 to the tan term:

Recall Pythagorean theorum:
Therefore:

Which proves:
Prove:
Recall:

Square both:

Add 1 to the cot term:

Recall Pythagorean theorum:
Therefore:

Which proves:
4. Compound & Double Angle Identities
Compound Angle:

Double Angle:
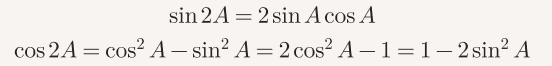
Example:
Evaluate
First, express as a sum of known angles
We can use a compound angle identity to break this down.
Use the compound angle identity for sine:
Using (recall) known values:

Substitute back in:

Simplify:

Final answer:

Contact Koyani Education for more worked examples, or any further guidance.
Book a tutoring session directly with our expert qualified teachers to guide you through your A-Levels and get you confidently prepared for your exams.
